understanding back propagation

2016-03-16

8 minute read

接下来的posts可能会focus在deep learning这一块，可能是真的太火了，觉得自己也得具备这个基本的知识库。自己也算是初学，望大家指点。

在neutral network的training中 back propagation 算法很关键我的学习方式是决定直接读 Hindon的那片文章《Learning representations by back-propagating erros》

对于learning system的描述直接翻译一小段

最简单的分层网络学习过程通常是：最低层是输入单元，有任意数目的中间层，最高层是输出单元，每一层内单元的不会有互联，也不会有跨层的互联，但是可以跳过这些中间层。一个输入向量就是设置输入单元的状态。每一层的单元的状态就是根据底下一层的输出当作输入由方程(1)和(2)来计算。每一层的计算被当作是并行，但是层与层之间是串行，这样自底往上的计算知道输出单元被决定。

假设一个 linear 的系统 input-output function

$x_{j} = \sum_{i} y_{i} w_{j i} (1)$

$x_{j}$ 是对unit $j$ 的全部输入， $y_{i}$ 是unit $i$ 的输出通过一个权重 $w_{j i}$ 连接到unit $j$ 上

到state的mapping输出通常是一个non-linear函数

$y_{j} = \frac{1}{1 + e^{- x_{j}}} (2)$

$x_{j}$ 是这个单元的所有输入

其实觉得这里的notation不是很好，不利于后面的思考，读者不妨把 $j$ 想象成是当前层，而 $i$ 是之前的那一层就行了这里的意思就是说前一层的输出经过加权就是这一层的输入，然后再经过方程(2)转成这一层的输出，方程(2)相当于模拟了神经元这是一个sigmoid函数方程(1)还可以加bias这里为了简洁没有写入. 根据 Hinton的 paper 里说的，第一个函数可以是任意的，只要有 bounded derivative，但是一般用一个linear function来combine inputs 到一个unit再用 non－linear 能够简化这个学习的过程。

那么学习的过程其实就是找到一组 weights 能够确保每一组输入对应的输出能够尽最大可能的贴近真值。

如果有有限的输入和输出，那么总的错误 $E$ 可以表示为

$E = \frac{1}{2} \sum_{c} \sum_{j} (y_{j, c} - d_{j, c})^{2} (3)$

其中 $c$ 是所有训练输入的index， $j$ 是输出的index， $y$ 是实际的输出 $d$ 是期待的输出

要想最小化 $E$ ，首先需要求导这样可以用梯度下降的方法因为我们的未知数是权重，而权重是一个向量，因此对于每一个维度，我们是求一个偏导

这里有一个 forward pass 是 equations (1)和(2)：每一层的states是尤其从前一层得到的输入来决定的

而 back pass 是指从最高层到最低层来传播的。

back pass 始于从 Error function (3) $E$ 来求对 $y$ 的偏导

$\partial E / \partial y_{j} = y_{j} - d_{c}$

这里有求导的 chain rule 因为我们知道

$\frac{\partial E}{\partial x_{j}} = \frac{\partial E}{\partial y_{j}} \cdot \frac{d y_{j}}{d x_{j}}$

带入方程 (2)

$\frac{(1 + e^{- x})^{- 1}}{d x} = \frac{- 1 \cdot (1 + e^{- x})^{- 2} d (1 + e^{- x})}{d x}$

$\frac{d (1 + e^{- x})}{d x} = \frac{d (e^{- x})}{d x} = \frac{e^{- x} d (- x)}{d x} = - e^{- x}$

很多年没做过chain rule求导了差点脑死亡

结果是稍作变形

$\frac{\partial E}{\partial x_{j}} = \frac{\partial E}{\partial y_{j}} \cdot \frac{e^{- x}}{(1 + e^{- x})^{2}} = \frac{\partial E}{\partial y_{j}} \cdot y_{j} (1 - y_{j}) (5)$

这个结果的含义是我们知道了当前层的 $j$ th unit的total input $x$ 如何影响 error 因为 $y_{j}$ 可以完全用 $x_{j}$ 表示, 然后这个 $x_{j}$ 其实是由之前一层的( $y_{i}$ )的线性加权 $w_{j i}$ 所以可以进一步的求出这些state和权重对于error 的影响。

同样的对于 $w_{j i}$ 表示是前一层 index $i$ 到这一层 index $j$ 的 weight

$\frac{\partial E}{\partial w_{j i}} = \frac{\partial E}{\partial x_{j}} \cdot \frac{d x_{j}}{d w_{j i}} = \frac{\partial E}{\partial x_{j}} \cdot y_{i} (4)$

表示 weight $w_{j i}$ 和前一层state 对于 error 的影响

此外还有前一层 unit $i$ 的输出 $y_{i}$ 对于 $\frac{\partial E}{\partial y_{i}}$ 的从前一层 $i$ 到这一层 $j$ 的贡献， $\frac{\partial E}{\partial x_{j}} \frac{\partial x_{j}}{\partial y_{i}} = \frac{\partial E}{\partial x_{j}} \cdot w_{j i}$

所以做一个summation就是前一层unit $i$ 发射出的所有connection

$\frac{\partial E}{\partial y_{i}} = \sum_{j} \frac{\partial E}{\partial x_{j}} \cdot w_{j i} (6)$

现在我们知道如何为倒数第二层计算 $\frac{\partial E}{\partial y_{i}}$ 当我们知道最后一层的 $\frac{\partial E}{\partial y_{j}}$ 的话

因为 $\frac{\partial E}{\partial y_{i}} = \sum_{j} \frac{\partial E}{\partial x_{j}} \cdot w_{j i} = \sum_{j} \frac{\partial E}{\partial y_{j}} \cdot y_{j} (1 - y_{j}) \cdot w_{j i}$

因此我们可以不停的向前计算结合当前层和前一层之间的权重得到前一层 $\frac{\partial E}{\partial y}$ ，用方程 (4)可以来计算 $\partial E / \partial w$

一开始 weight 都是 random 选取的

更新 weight 的方式，有每输入一组input-output case就更新这样不需要存导数

另一种是在输入 input-output case的过程先accumulate $\partial E / \partial w$ 直到全部输入完再更新权重

这里就用梯度下降每次减少一点点 $Δ w = - ε \partial E / \partial w$ 这个虽然没有二阶导下降的快，但是简单好实现容易用硬件来并行计算

一种改进是用当前的gradient来修改其在 weight space 的速度而不是position $Δ w (t) = - ε \partial E / \partial w (t) + α Δ w (t - 1)$ $t$ 每次sweep through the whole set of input-output cases, 加1

$α$ 是 exponential decay factor (0-1)，

Example

接下来用代码来验证一下代码中标记了和上面方程式的对应关系。

Network如图

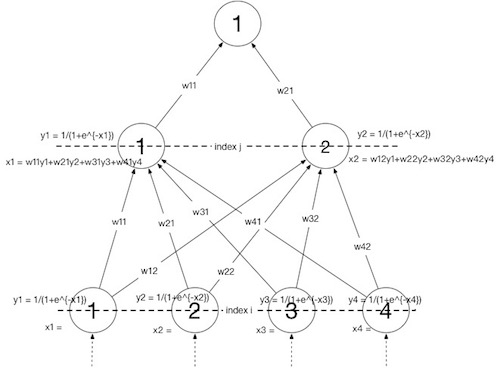
Network

Code

{% gist yishanhe/79f06cfa94b0e692698a %}

cost output

[ 0.02553798]
[ 0.02085472]
[ 0.01765256]
[ 0.01538757]
[ 0.01374046]
[ 0.01251489]
[ 0.01158523]
[ 0.01086832]
[ 0.01030757]
[ 0.00986344]
[ 0.00950775]
[Finished in 0.393s]

Example

Code

Reference